Περιεχόμενο

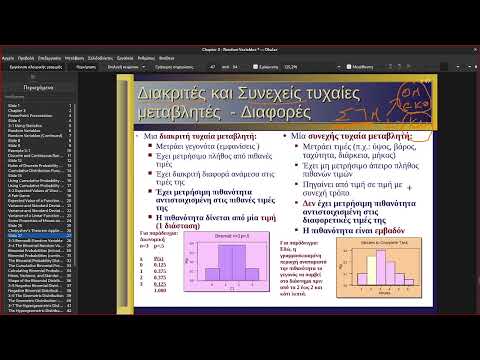
Τα συνεχή και διακριτά δεδομένα είναι αναπαραστάσεις πληροφοριών που χρησιμοποιούνται ευρέως στην επιστημονική έρευνα. Ενώ η αντίστοιχη χρήση οποιουδήποτε τύπου δεδομένων εξαρτάται γενικά από τη φύση των προς μετάδοση πληροφοριών, υπάρχουν ορισμένες περιπτώσεις όπου τα συνεχή δεδομένα μπορούν να αναλυθούν σε διακριτά δεδομένα. Με απλά λόγια, τα συνεχή δεδομένα είναι η αναπαράσταση πληροφοριών που έχουν αξία σε ολόκληρο τον τομέα, ενώ η διακριτή έχει αξία μόνο σε συγκεκριμένα σημεία. Ένα ευρέως χρησιμοποιούμενο παράδειγμα είναι η διαφορά μεταξύ ψηφιακών και αναλογικών πηγών δεδομένων.
Πηγή δεδομένων
Σε πολλές περιπτώσεις, η πηγή δεδομένων καθορίζει εάν οι πληροφορίες θα αναπαρασταθούν με συνεχή ή διακριτό τρόπο. Για παράδειγμα, οι ψηφιακές πληροφορίες, όπως αρχεία που είναι αποθηκευμένα σε ένα δίσκο, αντιπροσωπεύονται από μια σειρά 1 και 0. Αυτές οι πληροφορίες δεν έχουν καμία αξία μεταξύ αυτών των σημείων και, ως εκ τούτου, πρέπει να αντιπροσωπεύονται από έναν διακριτό τύπο δεδομένων. Τα συνεχή δεδομένα, όπως το ημιτονοειδές κύμα που δημιουργείται από έναν παλμογράφο, έχουν αξία σε όλα τα σημεία του τομέα, ανάλογα με το σημείο στο οποίο εξετάζεται.
Οπτικοποίηση δεδομένων
Τα συνεχή δεδομένα αντικατοπτρίζονται σε ένα γράφημα όπου όλα τα σημεία έχουν σημαντικές τιμές. Ένα παράδειγμα αυτού θα ήταν το τριγωνομετρικό ημιτονοειδές κύμα. Τα διακριτά δεδομένα, με τη σειρά τους, αντιπροσωπεύονται από ορισμένα σημεία, συνήθως πάνω από τους ακέραιους αριθμούς, σε ένα γράφημα. Παρόλο που μερικές φορές υπάρχουν γραμμές που συνδέουν αυτά τα σημεία, δεν αντιπροσωπεύουν τιμές σε αυτά τα σημεία σε ολόκληρο τον τομέα, χρησιμεύοντας μόνο ως τάσεις ή κατά μέσο όρο γραμμές μεταξύ αλλαγών στις τιμές τομέα.
Βοηθητικά προγράμματα
Οι συνεχείς συναρτήσεις, οι εξισώσεις που αντιπροσωπεύουν συνεχή δεδομένα, είναι τα κύρια εργαλεία των μαθηματικών. Αυτές οι λειτουργίες σάς επιτρέπουν να προσδιορίσετε τονικότητα, καθώς και άλλες σημαντικές πληροφορίες, όπως η κλίση και η εγγενής αξία. Οι διακριτές συναρτήσεις, που συνήθως εμφανίζονται με τη μορφή άπειρων σειρών, χρησιμοποιούνται ευρέως ως προσεγγίσεις όταν μια συνεχής λειτουργία δεν μπορεί να αναγνωριστεί σωστά. Σας επιτρέπουν επίσης να αναλύετε και να λαμβάνετε σημαντικές πληροφορίες από μη συνεχείς πηγές δεδομένων, όπως η μέση ημερήσια θερμοκρασία.
Λειτουργίες
Οι συνεχείς συναρτήσεις χρησιμοποιούνται σε υψηλό επίπεδο χειρισμού στα μαθηματικά. Για παράδειγμα, ένα από τα προαπαιτούμενα για ενοποίηση και λειτουργίες παραγώγων είναι ότι η συνάρτηση είναι συνεχής. Τα συνεχή δεδομένα λαμβάνονται επίσης εύκολα για φυσικά φαινόμενα. Για παράδειγμα, πολύ λίγα φυσικά φαινόμενα, όπως αλλαγές θερμοκρασίας, χρόνου και ήχου, εμφανίζονται διακριτικά. Τα διακριτά δεδομένα συχνά λένε πώς καταγράφονται τα φαινόμενα και επιτρέπει προσεγγίσεις, όπως μέσω της σειράς Taylor και Maclaurin, για συνεχή δεδομένα. Ένα καλό παράδειγμα αυτού είναι η προσέγγιση της ημιτονοειδούς λειτουργίας. Οι υπολογιστές χρησιμοποιούν τη σειρά Maclaurin για να προσεγγίσουν μια έγκυρη απάντηση για αυτήν τη λειτουργία, καθώς οι ψηφιακές συσκευές δεν μπορούν να επεξεργαστούν συνεχή δεδομένα.